Zadání soutěžních úloh

Časopis MATFYZIN

max. 55 bodů

Pracujete jako grafik časopisu MATFYZIN. Vaším úkolem je z příspěvků různých autorů vytvořit časopis podle předlohy v souboru časopis_matfyzin.pdf.

Příspěvky jsou uloženy ve složce úkol1_časopis a je třeba z nich odebrat hypertextové odkazy a opravit překlepy.

Formát časopisu:

• velikost strany A4
• zrcadlové okraje; vnitřní okraj 3 cm, vnější 2 cm
• základní text: font Cambria, velikost 12
• mezera za odstavcem: 12 bodů
• řádkování jednoduché
• zarovnání textu do bloku
• velikost písma nadpisu: 20 bodů
• je dodrženo pravidlo, že na konci řádku není jednopísmenková předložka
• na všech listech kromě prvního je v zápatí vloženo číslo stránky (pravý okraj) a text 3/2016 MATFYZIN (levý okraj)

UPŘESNĚNÍ K JEDNOTLIVÝM STRANÁM ČASOPISU

1. STRANA

Všimněte si znaku vloženého v textu:

2. STRANA

Věnujte pozornost indexům, řeckému písmenu kapa, konstantě a vzorci. Nejsou ve zdrojovém textu.

3. STRANA

Vložte poznámky pod čarou ke slovům LIGO a LISA.
Poznámka ke slovu LIGO: Interferometr pro hledání gravitačních vln
Poznámka ke slovu LISA: Připravovaný projekt pro detekci gravitačních vln

4. STRANA

Stránka je otočena na šířku

5. STRANA

Ze slova gravitace (první slovo odstavce na stránce) vytvořte hypertextový odkaz na: http://www.csfd.cz/film/275420-gravitace/prehled/

Věnujte pozornost číslům a vzorci v části Soutěžní úkol.

Výpočet tíhového zrychlení

max. 47 bodů

Honza se rozhodl změřit místní tíhové zrychlení g. Využil k tomu volného pádu. Ze vztahu s = \frac{1}{2} \cdot g \cdot t^2 si odvodil, jak ho vypočítat. Vyšel mu tento vzorec: g = 2 \cdot \frac{s}{t^2}. V tomto vzorci písmeno s znamená dráhu, kterou urazí těleso a písmeno t čas, tj. dobu pohybu tělesa. Provedl 60 měření. Kuličku pouštěl z výšky 2 m, 3 m a 4 m. Výsledky měření si zapisoval do sešitu. Při přepisování do poznámkového bloku v počítači si nedal pozor a měření zapsal neuspořádaně. Každé měření zapsal na samostatný řádek ve tvaru výška mezera čas.

1. Importujte data ze souboru data.txt do tabulkového kalkulátoru. Pokud neumíte data importovat, pracujte se souborem mereni.xlsx. (Soubory najdete ve složce úkol2/.)
2. Vypočítejte tíhové zrychlení g pro každé měření. Vzorec pro výpočet zapište do dalšího sloupce v tabulce. Sloupec nadepište „tíhové zrychlení“
   pomůcka: t^2 = t*t, použijte závorky
3. Vložte nový sloupec, ve kterém budou vypočítané hodnoty tíhového zrychlení g zaokrouhlené na 3 desetinná místa. Použijte k tomu vhodnou funkci (ne pouhé zobrazení čísla).
4. Vypočítejte průměr ze zaokrouhlených hodnot. (Kdo nemá zaokrouhlené, může počítat z vypočítaných hodnot.) Vzorec vložte pod tabulku do příslušného sloupce.
5. Vypočítejte odchylku každého měření. Odchylku zjistíte jako rozdíl mezi průměrnou hodnotou zrychlení a vypočítaným zrychlením g pro každé měření.
6. V našich zeměpisných šířkách je g = 9,81 ms^{-2}. Do dalšího sloupce vložte takový vzorec, který vypíše +, pokud je vypočítaná hodnota větší než 9,81, v ostatních případech vypíše -.
7. Do dalšího sloupce vložte takový vzorec, který vypíše text „přesné měření“, pokud se vypočítaná hodnota nachází v intervalu hodnot 9,8 až 9,9. V ostatních případech zůstane buňka prázdná.
8. Ukotvěte příčku tak, aby při rolování zůstával zobrazen řádek s popiskem výška, čas, atd.
9. Určete pomocí vzorce, jaký největší čas Honza naměřil. Vložte jej pod tabulku do sloupce, ve kterém je čas.
10. Určete, při kolika pokusech tento největší čas naměřil. Použijte vzorec, nepočítejte „ručně“! Výsledek vložte také pod tabulku.
11. Pomocí podmíněného formátování (světle modrá barva výplně buňky) zvýrazněte všechna měření s časem t < 0,65 \text{ s}.
12. Zkopírujte na druhý list jen sloupce obsahující výsledky měření, tj. sloupce vyska (m), cas (s).
13. Přejmenujte listy. První list na 1. výpočet, druhý list na 2. seřazení.

Následující úkoly zpracovávejte na druhém listu.

14. Seřaďte data podle údajů o výšce výšky a dále podle času vzestupně.
15. Vypočítejte průměr času pro každou měřenou výšku zvlášť. K tomu si do tabulky vložte volné řádky.
16. Pro jednotlivé výšky vypočítejte tíhové zrychlení g, vzorec vložte do řádku, ve kterém jsou vypočítané průměry. K jeho výpočtu použijte již vypočítané průměrné hodnoty času. Výsledek zobrazte na 2 desetinná místa.

Následující úkol zpracovávejte na třetím listu

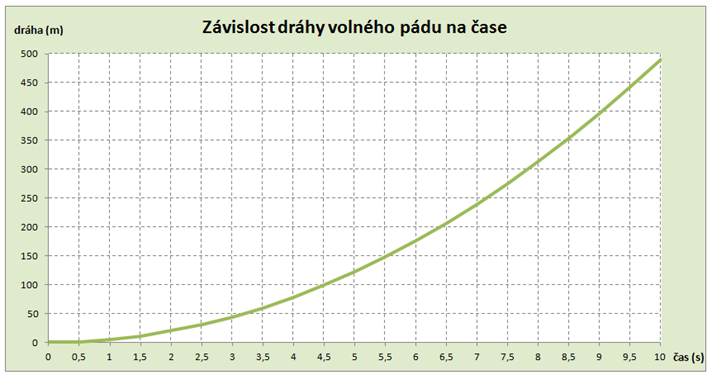
Třetí list pojmenujte 3. graf. Na tomto listu vytvořte graf podle následujícího zadání.

17. Graf závislosti dráhy volného pádu na čase.

    Vstupní hodnoty umístěte do tabulky. Tabulka bude zachycovat délku dráhy volného pádu pro časy od 0 sekund do 10 sekund s krokem půl sekundy.

    1. Do prvního sloupce tabulky zapište časy.
    2. Do druhého sloupce tabulky vypočítejte dráhu volného pádu s = \frac{1}{2} \cdot g \cdot t^2 (Pro výpočet použijte hodnotu g=9,81 ms^{-2}.)
    3. Do třetího sloupce zaokrouhlete výsledky na celé metry.
    4. Pro sestrojení grafu použijte zaokrouhlené hodnoty. (poznámka: nemáte-li zaokrouhleno, sestrojte graf z vypočítaných hodnot)
    5. Sestrojte graf. Zformátujte ho podle předlohy.
       

Propagace časopisu

max. 17 bodů

Svůj časopis vytvořený v první úloze máte propagovat formou prezentace. Vytvořte tedy prezentaci věnovanou článkům z časopisu.

• Informace čerpejte z materiálu pro úkol v textovém editoru
• V prezentaci informujte o třech článcích – každému článku jsou věnovány dva snímky
• Nepoužívejte žádný motiv (tj. předefinovaný vzhled prezentace), ale vytvořte si vlastní grafický návrh, nejlépe s využitím předlohy snímku.
• Prezentaci zpracujte podle pravidel pro tvorbu prezentace
• Zvolte vhodně animace či přechody snímků

Obsah snímků:

1. snímek – úvodní snímek prezentace

2. snímek – obsahuje rozcestník tj. názvy článků, o kterých v prezentaci informujete.
Každý z těchto názvů je hypertextovým odkazem, který vede na snímek věnovaný danému tématu.

3.–8. snímek – obsahují informace o článcích z časopisu. jeden článek = 2 snímky
Na každém jsou vložena dvě tlačítka (nebo tvary).

• První z nich odkazuje na 2. snímek, tj. na rozcestník
• Druhé tlačítko ukončí prezentaci

Na všechny snímky vložte zápatí a do něj své jméno.