Prasátko
Koeficient 1
Vytvořte program, který zobrazí prasátko podobné tomu na
následujícím obrázku:
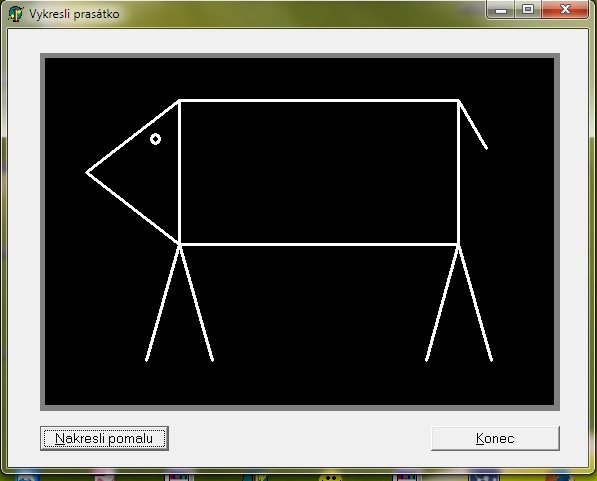
Program bude pracovat tak, že postupně zobrazuje jednotlivé
úsečky (a kružnici) tvořící obrázek prasátka. Prodleva
mezi zobrazením jednotlivých úseček bude 0,5 s.
Posloupnost zobrazení není důležitá a nebude se hodnotit.
Při změně velikosti základního okna obrázek překreslete tak,
že zachovává původní proporce prasátka (šířka čar přitom zůstává stejná).
Nadstavbovou funkcí programu je pomalé (animované)
vykreslení jednotlivých úseček tvořících prasátko:
- Každá úsečka plynule prodlužuje délku z 0 na svou konečnou velikost.
- Animace musí být postřehnutelná lidským okem –
vykreslení jedné úsečky musí trvat minimálně 1 s a maximálně 3 s.
- Pro odlišení zobrazovacího režimu použijte jinou barvu
úseček než při základním zobrazení.
- Umožňete při vykreslování obrázku kdykoliv přerušit
animované zobrazování. Na konci animace zobrazte celé prasátko
v původní barvě.
Pro inspiraci je připravena ukázková aplikace (funguje v operačním systému Windows).
Hodnocení
| Body |
Za co |
| 1 |
program lze spustit - zobrazení prasátka |
| 1 |
zobrazení prasátka postupně po jednotlivých úsečkách |
| 2 |
změna velikosti obrázku prasátka při zachování proporcí |
| 4 |
animace - pomalé vykreslení jednotlivých úseček |
| 1 |
možnost přerušit kdykoliv animaci |
| 1 |
dokumentace |
Sčítání zlomků
Koeficient 1
Jakub se vrací ze školy celý smutný – za domácí úkol musí
s využitím Eukleidova algoritmu spočítat spoustu příkladů se zlomky.
Postup ve škole celkem pochopil, ale kdo mu zkontroluje, že má příklady
spočítané správně? Pomozte Jakubovi, aby si příklady mohl zkontrolovat sám
a nemusel už věšet hlavu! Takovouto činnost by měl přece zvládnout
jednoduchý program.
Každý příklad na sečtení dvou zlomků vypadá následovně:
\frac{a}{b} + \frac{c}{d} = x + \frac{y}{z}
kde a, b, c, d, x, y
a z jsou celá kladná čísla. Dále platí, že čitatel je nesoudělný
s jmenovatelem (zlomky jsou pokráceny) a také
a < b, c < d
a y < z. Pokud je součtem zlomků celé číslo, pak
y = 0 a na z nezáleží.
Vypracujte program, který načte hodnoty a, b, c
a d ze vstupního souboru a výsledné hodnoty x,
y a z zapíše do výstupního souboru.
Popis vstupu
Vstup načtěte ze souboru zadani.txt v aktuálním
adresáři.
Každému příkladu odpovídá jedna řádka, tedy vstupní soubor
zadani.txt na jedné řádce obsahuje vždy čtyři čísla oddělená
mezerou. Řádky jsou ukončeny dvojicí znaků CR
a LF. Předpokládejte, že příkladů bude méně než dvacet.
Dále pro jednoduchost předpokládejte, že čísla a, b,
c a d jsou menší než 109.
Popis výstupu
Výstup zapište do souboru vystup.txt v aktuálním
adresáři.
Každému příkladu odpovídá jedna řádka, tedy výstupní soubor bude
obsahovat na jedné řádce vždy tři čísla oddělená mezerou.
Řádky ukončete dvojicí znaků CR a LF.
Příklad vstupu, výstupu a ilustrativní zobrazení
Příklad vstupního souboru zadani.txt:
1 5 4 5
2 3 2 3
1 3 1 3
1 5 7 8
8 15 4 5
63 1310400 31423 72225
Příklad výstupního souboru vystup.txt, který odpovídá
výše uvedenému zadani.txt:
1 0 0
1 1 3
0 2 3
1 3 40
1 1 3
0 1045873 2403648
Ilustrativní zobrazení pro výše uvedený vstup a výstup:
| Vstup |
Výstup |
Ilustrativní zobrazení |
| 1 5 4 5 |
1 0 0 |
1/5 + 4/5 = 1 |
| 2 3 2 3 |
1 1 3 |
2/3 + 2/3 = 1 + 1/3 |
| 1 3 1 3 |
0 2 3 |
1/3 + 1/3 = 0 + 2/3 |
| 1 5 7 8 |
1 3 40 |
1/5 + 7/8 = 1 + 3/40 |
| 8 15 4 5 |
1 1 3 |
8/15 + 4/5 = 1 + 1/3 |
| 63 1310400 31423 72225 |
0 1045873 2403648 |
63/1310400 + 31423/72225 = 0 + 1045873/2403648 |
Ukázkové soubory pro testování vašeho programu najedete v adresáři
zlomky.
Hodnocení
| body |
za co |
| 0,5 |
program lze spustit |
| 0,5 |
program načítá čísla ze vstupního souboru
zadani.txt |
| 0,5 |
program zapisuje výstupní soubor vystup.txt
ve správném formátu
|
| 0,5 |
za každý správně spočtený příklad (je jich celkem 15) |
| 1 |
dokumentace, komentáře, přehlednost, … |
Domino
Koeficient 2
Z dominových kostek vytvořte co nejdelší na sebe navazující řadu za
předpokladu, že dominové kostky můžete otáčet. Body dostanete podle
délky nalezené řady. Lze tedy získat body i v případě, že váš program nenalezne
nejdelší možnou řadu. Program by měl najít řešení do několika vteřin.
Například z kostek [1:3], [1:3],
[4:5], [3:3] a [0:5] lze vytvořit
řadu [1:3][3:3][3:1] (a dvě kostky zbudou).
Řad lze většinou vytvořit více, ale vy máte za úkol najít libovolnou z nich, hlavně
musí být co nejdelší.
Vstupem bude textový soubor, ve kterém každé kostce odpovídá jeden zápis ve tvaru
[a:b], kde a a b jsou celá čísla z intervalu od 0 do 6.
Počet dominových kostek ve vstupním souboru je minimálně jedna a maximálně
1000. Všechny dominové kostky jsou zapsány bez mezer na jednom řádku.
Výstupem bude textový soubor, ve kterém budou uvedeny vybrané (a správně
natočené) na sebe navazující kostky ve tvaru [a:b], například:
[1:3][3:3][3:1]
Mezery ve výstupním souboru se ignorují, ale vypište prosím všechny
kostky bez mezer na jeden řádek.
Výsledný soubor se bude vyhodnocovat programově. Proto je potřeba
zachovat předepsaný tvar – viz soubory reseni_soutezici[1-9].txt.
Část bodů bude přidělena i v případě, že nedosáhnete maximální možné délky.
Pro kontrolu vámi vytvořených řešení máte k dispozici validační program
validace_soutezici.html,
který po otevření v prohlížeči vyhodnotí vaše řešení libovolné z úloh
zadani_soutezici[1-9].txt.
Ukázkové soubory se zadáním a jedním z možných nejdelších řešení
naleznete v adresáři domino.
Hodnocení
Pro porotu jsou určeny soubory
zadani_porota[1-9].txt a
reseni_porota[1-9].txt v adresáři domino.
Při vyhodnocení spusťte program soutěžícího na testovací data. Program by
měl skončit do pěti vteřin. Výsledný soubor nakopírujte do dodaného validačního
programu validace_porota.html
a vyberte správné číslo testovacích dat. Validační program zkontroluje, zda
je řešení správné, a pokud je, stanoví počet bodů, které soutěžící za tato
data obdrží.
| Body |
Za co |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota1.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota2.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota3.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota4.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota5.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota6.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota7.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota8.txt |
| 1 |
nalezení nejdelšího řetězu na vstupu zadani_porota9.txt |
| 1 |
Komentáře, přehledný kód, popis algoritmu, názvy proměnných. |
Meteorologická data
Koeficient 2
Vědět nebo aspoň tušit, jaké bude počasí je určitě dobrá věc,
naši předkové k tomu používali prognostiky, něco jako Medardova
kápě, 40 dní kape nebo Na Svatého Jiří vylézají hadi a
štíři… Doba ale pokročila a nám s předpovědí počasí pomáhají
nové moderní metody. Jednou z nich je i sledování naměřených
hodnot za poslední roky a určování pravděpodobného počasí na
základě naměřených dat.
Vaším úkolem bude napsat program, který načte meteorologická data ze vstupního souboru,
následně je zpracuje, vyhodnotí a umožní uživateli si je prohlédnout v grafické podobě.
Vstupní soubor obsahuje data od 1. ledna 1975 do
31. prosince 2014, vždy jedno měření pro každý kalendářní
týden v daném roce. Váš program by měl umožnit uživateli
následující:
- Načtení meteorologických dat ze vstupního souboru.
- Zadání časového úseku ve formě
týden/rok od
– týden/rok
do
(například tedy 12/1975–15/1975), pro který se mají
zobrazit meteorologická data.
- Pro zadaný časový úsek vykreslit spojnicový graf, který bude ukazovat čtyři křivky:
- Maximální teplotu – červenou barvou
- Minimální teplotu – modrou barvou
- Průměrnou teplotu – zelenou barvou
- Naměřenou teplotu – žlutou barvou
Ukázka grafu:
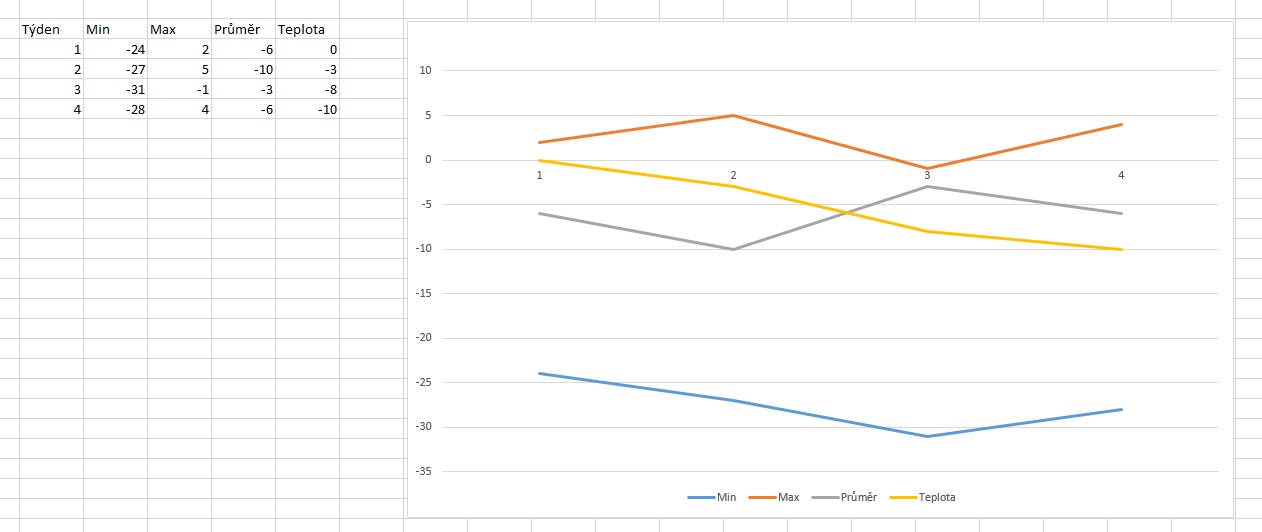
- Maximální teplota – maximální teplota pro daný kalendářní
týden za celé období, pro které máme data.
- Minimální teplota – minimální teplota pro daný kalendářní
týden za celé období, pro které máme data.
- Průměrná teplota – průměrná teplota pro daný kalendářní
týden za celé období, pro které máme data.
- Naměřená teplota – teplota, která je pro daný kalendářní
týden uvedena v souboru.
Na vstupu obdržíte CSV soubor, formát vstupních dat je
následující:
Rok;Týden;Teplota
1975;1;14
1975;2;15
1975;3;27
1975;4;6
1975;5;14
1975;6;19
1975;7;-21
…
2014;52;-93
Na první řádce jsou názvy údajů. Následuje libovolný počet řádek,
kde jsou postupně uvedené rok, týden a teplota oddělené
středníkem. Řádky jsou ukončené znaky CR a LF.
Ukázkový soubor: meteodata/meteodata.csv.
Pro jednoduchost počítejte s tím, že každý rok má 52 týdnů, k dispozici jsou hodnoty
za posledních 40 let (tj. od roku 1975), máte k dispozici hodnoty pro každý týden
v roce (měření proběhlo vždy ve středu v každém týdnu).
Přibližnou ukázku toho, jak mají grafy vypadat, si můžete vyzkoušet
v jednoduché ukázkové aplikaci – meteodata/Meteodata.jar.
Hodnocení
Nechceme pro porotu a soutěžící jiná data?
| Body |
Za co |
| 1 |
Program lze spustit |
| 1 |
Lze vybrat vstupní soubor |
| 1 |
Je možné zadat rozmezí kalendářních týdnů, pro zobrazení grafu |
| 1 |
Program zobrazí správně spojnicový graf pro rozmezí 3 týdnů (1/1975 - 3/1975) - obr.
1
|
| 1 |
Program zobrazí správně spojnicový graf pro rozmezí 5 týdnů (47/2014 - 51/2014) -
obr. 2
|
| 1 |
Program zobrazí správně spojnicový graf pro minima hodnot 3 týdnů (10/2000 - 13/2000)
- obr. 3
|
| 1 |
Program zobrazí správně spojnicový graf pro maxima hodnot 3 týdnů (20/2005 - 23/2005)
- obr. 4
|
| 1 |
Program zobrazí správně spojnicový graf pro průměrné teploty v rámci 3 týdnů (41/2010
- 44/2010) - obr. 5
|
| 1 |
Program vyhlásí chybu pro špatně zadaný časový úsek (kalendářní týden menší než 1/1975
nebo větší než 52/2014)
|
| 1 |
Komentáře, přehledný kód, ... |

